Affine Multiplexing Networks: System Analysis, Learning, and Computation
I. Papusha, U. Topcu, S. Carr, and N. Lauffer
- Manuscript
- Presentation slides
- Toolbox (
amnet)
Abstract
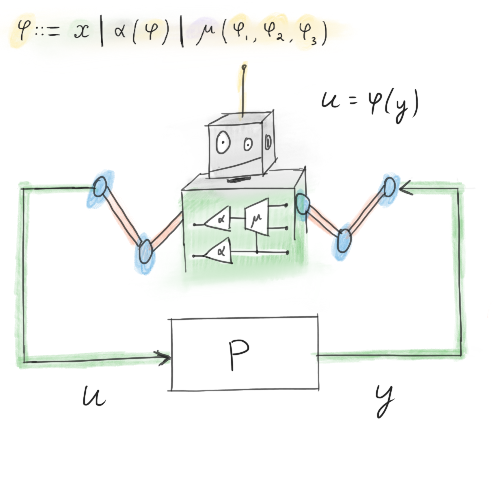
We introduce a novel architecture and computational framework for formal, automated analysis of systems with a broad set of nonlinearities in the feedback loop, such as neural networks, vision controllers, switched systems, and even simple programs. We call this computational structure an (AMN). The architecture is based on interconnections of two basic conceptual building blocks: multiplexers (μ), and affine transformations (α). When attached together appropriately, these building blocks translate to conjunctions and disjunctions of affine statements, resulting in an encoding of the network into satisfiability modulo theory (SMT), mixed integer programming, and sequential convex optimization solvers.
We show how to formulate and verify system properties like stability and robustness, how to compute margins, and how to verify performance through a sequence of SMT queries. As illustration, we use the framework to verify closed-loop, possibly nonlinear dynamical systems that contain neural networks in-the-loop, and hint at a number of extensions that can make AMNs a potent playground for interfacing between machine learning, control, convex and nonconvex optimization, and formal methods.
Citation
I. Papusha, U. Topcu, S. Carr, and N. Lauffer “Affine Multiplexing Networks: System Analysis, Learning, and Computation,” arXiv:1805.00164 [math.OC], 2018.